Go杂谈 | 高效数据编解码
序列化和反序列化贯穿于微服务系统之间,如何简单高效的处理数据变的异常重要。常见的数据编解码方案中Protobuf、Avro等算是其中的佼佼者。出色的编解码方案都有哪些特点呢?以及还有没有性能更优或者使用更简单的方法呢?我们来探究一下。
Varint & Zigzag
Varint
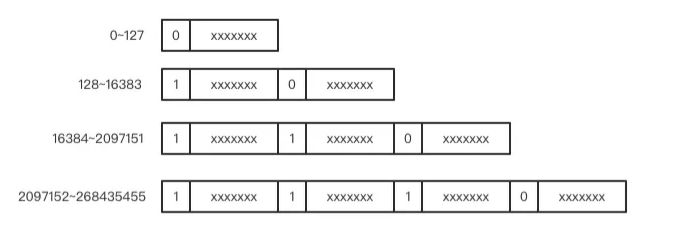
varint用每个字节的第1位来标识本字节是否是一个数的尾部,0代表是尾部,1代表需要利用后面的字节。这样每个字节实际有效是7位。方案示意图如下:
这种方案在小的正整数比较多的场合非常高效。可是当负整数的时候,因为负数在计算机中一般用其正数的补码形式表示,这导致varint编码需要占中10个字节,此时编解码性能极差。
Zigzag
计算机中的有符号数有三种表示方法,即原码、反码和补码。三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位,三种表示方法各不相同 [1]。在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。
对于计算机,其概念和方法完全一样。n位计算机,设所能表示的最大数是11111111,若再加1成为100000000(9位),但因只有8位,最高位1自然丢失,又回到了00000000(8位),所以8位二进制系统的模为2的8次方,在这样的系统中减法问题也可以化成加法问题。只需把减数用相应的补数表示就可以了。把补数用到计算机中数的处理上,就是补码。
比如 -5 这个数,在计算机中存储为 5 的补码形式:11111111 11111111 11111111 11111011 , Zigzag编码方式如下:
- 左移一位,即 “ 11111111 11111111 11111111 11110110 ”
- 符号位放到最后,即 “ 11111111 11111111 11111111 11110111 ”
- 除最后一位外全部取反,即 “ 00000000 00000000 00000000 00001001 ”
- 最后再使用Varint编码
Zigzag转换的代码实现如下:
|
|
| 编码前 | Zigzag编码后 |
|---|---|
| 0 | 0 |
| -1 | 1 |
| 1 | 2 |
| -2 | 3 |
| 2 | 4 |
| 2147483647 | 4294967294 |
| -2147483648 | 4294967295 |
就是将负数转换成相应正数的2倍减1,将正数转换成其值的2倍。
(未完待续…)
- 原文作者: 闪电侠
- 原文链接:https://chende.ren/2024/09/11171227-004-data-codec.html
- 版权声明:本作品采用 开放的「署名 4.0 国际 (CC BY 4.0)」创作共享协议 进行许可